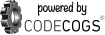Harvey Mudd Math Fun Facts

Harvey Mudd Professor Francis Su has put together a very nice collection of what he calls "Mudd Math Fun Facts," interesting puzzles that he uses to spice up his undergraduate math classes. As he says, they are "ideas that change the way you think." His facts are labelled by difficulty (easy, medium, or hard) and by the area of mathematics from which they are drawn (algebra, geometry, number theory, probability, calculus/analysis, and "other.")

Although designed for undergraduates, there are many gems in his collection that would be perfect for Albany Area Math Circle students who are working as MATHCOUNTS coaches or mentors to our motivated middle school students. What you might want to do is select 10 or so of these that you think your students might enjoy, print them out, cut the facts into separate strips, and put them in a bag or a box. Then, when your students need a quick change of pace, just draw one out at random, and get your students thinking about it. Make sure to think about these ideas yourself before you put them in the bag--you'll probably find you deepen your own problem-solving skills, especially if you think of extensions or generalizations. You might want to generate some of your own fun facts from cool puzzles you run across in other contexts.

Here's an example of a medium Mudd Math Fun Fact. You can find the answer here.

One hundred ants are dropped on a meter stick. Each ant is traveling either to the left or the right with constant speed 1 meter per minute. When two ants meet, they bounce off each other and reverse direction. When an ant reaches an end of the stick, it falls off.

At some point all the ants will have fallen off. The time at which this happens will depend on the initial configuration of the ants.

Question: over ALL possible initial configurations, what is the longest amount of time that you would need to wait to guarantee that the stick has no more ants?

Information cascades, herd instinct, and the wisdom (?) of crowds

Professor Orzel's coin estimation contest is now over, and the graph above shows his plot of the estimates submitted by people who entered the contest. The red vertical line shows the true correct value of $165.26. The median and mean of the guesses were $77.12 and $83.30, roughly half of the true value.

My own guess was based on a simple strategy: choose the middle of a large open interval that was on the high side of the 50 or so guesses already submitted by the time I entered. Why?

1) Stakes were low*, and it was rational for me not to spend a lot of time computing a complex estimate.

2) By the time I entered, a lot of people had already submitted guesses, most of which seemed grounded in plausible reasoning, so it was rational for me to "free ride" off their computational efforts.

3) I knew from the MBA study that, on average, people typically tend to underestimate the value of a bunch of coins, and Geeky Mom's recent post also reminded me of this tendency. On the other hand, the Bazerman-Samuelson experimental data also told me that there is usually at least one person who guesses too high.

4) So I wanted to guess high, but I didn't want to outflank the highest guesser.

5) And I wanted a large open interval so I could take the midpoint of that interval and hopefully "control" a large amount of numeric real estate. At the time I submitted my guess, I saw a large open interval on the highish side, running from $120.94 to $150.92, so I submitted a guess which was midway between those two points, which was $135.93. So, if nobody else had come along afterwards, I would have "controlled" the entire span between $128.43 and $143.43. (Of course, people did come along and poach on my real estate, but what can you do? It's a free country, as they say! Actually, if I'd been obsessive, I'd have waited until the last possible moment, in order to take all possible data from other people's guesses into account, but I'm not THAT obsessed!)

How did I do? Well, I didn't win. That honor went to Michael Day, who submitted a guess of $166.10. (At least he wasn't one of those folks poaching on my "turf.")

But at least I did better than the median or mean, and I also came closer than Professor Orzel himself, who said he would have guessed $130. And, of course, he had some informational advantages (what the SEC would call "insider information," if this were a marketable security.)

Professor Orzel asks:

Now, why were the rest of the guesses so far off? Isn't the "wisdom of crowds" effect supposed to make an average of a large number of estimates better than any individual guess?

As I mentioned in my last post, winner's curse is not a factor in this contest, because it's not an auction situation. In an auction, you would expect sophisticated bidders to bid somewhat on the low side, because they are worried about the winner's curse phenomenon.

However, as I pointed out before, Professor Orzel's contest isn't an auction, so there's no winner's curse involved. (If there HAD been an auction of the coin jar, it would most likely have been won by that person on the far right of the histogram, who thought the coins were worth $327. If everyone were rational, and took winner's curse into account, they would likely have bid less than their estimates. The question is whether they would have adjusted their bids ENOUGH.)

But the question remains: why is the average of the estimates in this case so far below the true value? (Even worse than the estimates of those Bazerman/Samuelson MBA students, whose estimates averaged about 65% of the true value.) At least they were better than Geeky Mom's estimate. (It would be interesting to see the data from her bank, which runs an estimation contest.)

A few possibilities include the phenomena known as information cascades or herd instinct.

Basically, what it comes down to is this: when people were submitting their guesses, they were using the information they had about other people's guesses in formulating their own guesses. That means that our guesses were not independent of one another. You see this sort of thing all the time in financial bubbles and panics. Of course, the stakes here were much lower* than in the global financial markets.

Now, it was entirely rational for us to use all the information we had available in formulating our own guesses, including the guesses submitted by other people, especially those of us who were sophisticated in how we used the data. (I like to think that I was reasonably sophisticated in my use of the information, even if I didn't win the contest!) But other people might have used the early information in more naive ways, because they didn't take into account the fact that people have a tendency to underestimate values of coin containers, which led to an unfortunately inaccurate information cascade.

*No offense intended with the "low stakes" remark, Prof. Orzel, but all of us losers will just have to wait a little while until your book hits the bookstore shelves. Having to wait a little to read your book is a lot less painful than what the information cascades have done to the world economy in past year.

Coin estimation contest and winner's curse

Union College Physics Professor Chad Orzel has a book coming out this fall, How to Explain Physics to Your Dog, which looks great, from what I have seen of the previews on his blog, Uncertain Principles.

You can win a free galley proof copy of his forthcoming book if you can correctly guess the dollar value of the change in his loose change box.



Details of his contest and a better picture are here.

Professor Orzel's contest reminded me of the famous coin-jar auction experiments that a psychologist and an economist conducted with their MBA students to illustrate the winner's curse phenomenon, an important concept in game theory, a branch of applied mathematics.

Robert Frank's Behavioral Economics text describes those experiments as follows:

[When] psychologist Max Bazerman was teaching at Boston University some years back, he and his colleague William Samuelson performed the following experiment in their microeconomics classes. First they placed $8 worth of coins in a clear jar. After giving their students a chance to examine the jar carefully, they then auctioned it off--coins and all--to the highest bidder. They also asked each student to submit a written estimate of the value of the coins in the jar.

On the average, students behaved conservatively, both with respect to their bids and to the estimates they submitted. Indeed, the average estimate was only $5.13, about one-third less than the actual value of the coins. Similarly, most students dropped out of the bidding well before the auction price reached $8.

Yet the size of the winning bid in any auction depends not on the behavior of the average bidder, but on the behavior of the highest bidder. In 48 repetitions of this experiment, the top bid averaged $10.01, more than 20 percent more than the coins were worth.

Professor Frank goes on to note that: "Bazerman and Samuelson thus made almost $100 profit at the collective expense of their winning bidders. At that price, the winners may consider it an important lesson learned cheaply." Why? Because the winner's curse phenomenon can occur in real world situations with far greater stakes, for example, in oil lease auctions and corporate takeovers. For more information, see here and here.

However, as I noted above, Professor Orzel teaches physics, not psychology or economics, so there's no "winner's curse" risk in his contest, but you can still have fun thinking about your strategy for coming up with a guess.

More on coins

Geeky Mom writes:

Yesterday, I filled a bag with about half of the coins and trudge to the bank on my way to the farmer's market. The bank lets you estimate how much money you have and if you're close, you win a prize. As I poured the money into the machine, I saw mostly pennies. So, I estimated about 7.50. When it was all said in done, I had slightly over $52 in coins. Mostly dimes, it turned out. I'm really bad at estimating, especially now that I rarely handle cash, much less coins. All my cash is digital, exchanged either via electronic transfer or similarly, using my debit card. I used to keep tips in a mayonnaise jar on my dresser, saving up for the deposit on an apartment in graduate school town. I know about how much was there, in part because I knew how much I made in tips, but also because I dealt with cash all the time.

I spent a little more than half of my new found cash at the farmer's market. Even though I always take cash there (most of the vendors don't take other forms of payment), I felt a little giddy at having such a large amount, created, it seemed, out of thin air.

Money now does seem to come out of thin air, arriving in bank accounts without anyone having to touch anything. I used to work at a bank during the summers. One summer I filed loan applications, the 3 attached parts left after everything was signed off. Another summer I filed the checks people deposited into their accounts, checks that were then sent to other banks to be filed and then placed in an envelope to be sent to the customer with her statement. Even then, the real transaction happened electronically, with a machine reading routing and account numbers, a human inputting the amounts, which were then coded onto the check to be read by another machine. For a brief time each summer, it was my job to count money coming in from the vendors at the annual summer festival. Bags of coins and dollar bills showed up at the bank and I stood behind the tellers, counting it all by hand, recording amounts on deposit slips, amounts that were later entered into computers while the money itself went into the vault, to be redistributed to banks or to customers withdrawing money.

Her post captures how a lot of people have lost touch with their "number sense" about money, because most monetary transactions are about electrons zapping around from place to place.

It's actually very hard to pay your income tax bill in cash. Even if you walk into one of the few remaining IRS taxpayer assistance centers with a wad of twenty dollar bills trying to pay off your tax bill, they are reluctant to accept it. Basically, the IRS is just not set up to take cash. They really want you to use their electronic payments system or mail them a check. And don't even think about trying to pay your tax bill with a wheelbarrel full of pennies!

Ideally, what makes it as simple as possible for the IRS is for your employer to (slightly) overpay your taxes through withholding from your wages throughout the year, and then they'll send you a refund (preferably by direct deposit) after you file your tax return at the end of the year.

Today's Wall Street Journal has an op-ed from Charles Murray saying that this approach is "bad for Democracy."

He proposes that we replace the current system under which most American pay most of their taxes through withholding from their wages with a system under which all American taxpayers would instead just send in quarterly tax payments to the IRS.

You can read more about this in two recent posts on my tax policy blog.

Nice coin problem

Tanya Khovanova has posted a very nice fake coin weighing problem on her math blog.

It goes beyond the usual coin problem by introducing the concept of a "revealing coefficient." The idea is to solve the coin weighing problem in a way that gives away as little information as possible about the identity of which particular coins are fakes.

I've found one solution, which I've posted as a comment to her blog. It gives a revealing coefficient of about 78%. I suspect it's possible to do better, because I didn't think for very long before I came up with my solution. If you want to see if you can get a solution with a lower revealing coefficient, go to her post on Unrevealing Weighings and try it for yourself.

Update: I now realize that I misread the original problem, so my originally posted "solution" does not actually solve the problem. I've now posted a new solution that I think works--but I hope someone will post a more clever one that improves the revealing coefficient that my simple approach yielded.

Pentablocks and beautiful geometric puzzles

The NYC Math Circle facebook page asked:

What is the ratio of the blue area to the area of the whole regular star in this picture?

This problem has a very beautiful answer, but it's hard for most people to visualize, unless they have a lot of geometric intuition. You might want to try playing with it for a while before visiting the discussion in the NYC Math Circle Facebook page.

The Pentablocks I showed to the New York Math Circle Teachers summer workshop last week provide a very easy way to visually construct and/or confirm the solution to the problem above.



Pentablocks are a very nice way to develop your geometric intuition in understanding the relationships in pentagons, pentagrams, and related polygons, the golden ratio (phi), Penrose tilings (quasicrystals), and more. As their name suggests, Pentablocks are based on pentagons and pentagrams (five-pointed stars). All their angles are multiples of 18 degrees, and all their side-lengths are related to one another by the golden ratio, phi.

The more traditional (and easier to find) Pattern Blocks are based on hexagons. All their components have angles which are multiples of 15 degrees, and all their dimensions are related to one another by 1, 2, and the square root of 3.

You can use either set to tessellate, but the Pentablock tessellations are far more complex than the traditional pattern block tessellations.

I'll bring sets of both types of blocks to our Labor Day weekend picnic so you can explore more relationships with them.

More on the value of negative information

Professor Moorthy points out that this week's National Public Radio puzzle from Will Shortz is another good example of the value of negative information.

A waitress walks up to a breakfast table with five logicians and asks, "Does everyone here want coffee?"

The first logician says, "I don't know."

The second logician says, "I don't know."

The third logician says, "I don't know."

The fourth logician says, "I don't know."

And the fifth logician says, "No."

Who did the waitress bring coffee to — and why?

If you think you know the answer, you can visit the NPR Sunday Puzzle website to find out how to submit your answer for a possible chance to play their on-air puzzle game next Sunday.

The value of NEGATIVE information

The HangMath game, which I showed the NYC Math Circle teachers, is also an opportunity to talk about the importance of "negative information."

In other words, if someone has asked about "2's in the tens column," the game requires the emcee to fill in ALL the 2's in the tens column. An efficient information user should make use of negative information (i.e, the blanks that still remain blank in the ten's column do NOT contain 2's) as well as positive information (the blanks that have been filled in with 2's in the tens column DO
contain 2's.)

Thanks to a tip from Professor Moorthy, here's a link to a new twist on a classic puzzle about drawing inferences from negative information: The Case of the Pinocchio Politicians.

You can find many delightful related puzzles that use this kind of reasoning in Martin Gardner's The Unexpected Hanging and Other Paradoxes. Raymond Smullyan's awesome mathematical logic books also have many such puzzles.

Exponentials and superexponentials

What do you think are the odds that you will die during the next year? Try to put a number to it — 1 in 100? 1 in 10,000? Whatever it is, it will be twice as large 8 years from now.

This startling fact was first noticed by the British actuary Benjamin Gompertz in 1825 and is now called the “Gompertz Law of human mortality.” Your probability of dying during a given year doubles every 8 years. For me, a 25-year-old American, the probability of dying during the next year is a fairly miniscule 0.03% — about 1 in 3,000. When I’m 33 it will be about 1 in 1,500, when I’m 42 it will be about 1 in 750, and so on. By the time I reach age 100 (and I do plan on it) the probability of living to 101 will only be about 50%. This is seriously fast growth — my mortality rate is increasing exponentially with age.

And if my mortality rate (the probability of dying during the next year, or during the next second, however you want to phrase it) is rising exponentially, that means that the probability of me surviving to a particular age is falling super-exponentially. Below are some statistics for mortality rates in the United States in 2005, as reported by the US Census Bureau (and displayed by Wolfram Alpha):



This data fits the Gompertz law almost perfectly, with death rates doubling every 8 years. The graph on the right also agrees with the Gompertz law, and you can see the precipitous fall in survival rates starting at age 80 or so. That decline is no joke; the sharp fall in survival rates can be expressed mathematically as an exponential within an exponential:



Surprisingly enough, the Gompertz law holds across a large number of countries, time periods, and even different species. While the actual average lifespan changes quite a bit from country to country and from animal to animal, the same general rule that “your probability of dying doubles every X years” holds true. It’s an amazing fact, and no one understands why it’s true.

There is one important lesson, however, to be learned from Benjamin Gompertz’s mysterious observation. By looking at theories of human mortality that are clearly wrong, we can deduce that our fast-rising mortality is not the result of a dangerous environment, but of a body that has a built-in expiration date.

The excerpt above comes from a post in Gravity and Levity, a blog full of "big crazy ideas behind the equations" in physics. I highly recommend reading the entire post, which talks about how the curves would be shaped under different models of mortality--the author shows that the so-called "lightning bolt" and "accumulated lightning bolt" models of mortality are not consistent with the observed graphs above, but a "cops and criminals inside your body" model, rooted in cell biology, is consistent with the graphs above.